As kids, most of us probably remember being fascinated with huge numbers as soon as we learned how to count. I recall spending hours punching numbers into a calculator and being mesmerized at how quickly or slowly the numbers became huge. Try calculating the natural logarithm of the natural logarithm of a huge number, 
and watch how big the number must be for the result to be a big number too. Take for example, 
This is only about 
On the other hand, you can try calculating the factorial (exclamation symbol on a calculator) of a number, 
to see how quickly the numbers get huge. 
but by the time you reach 24 we have 
What I was fascinated with the most, however, was the idea of infinity. Every child envisions infinity when they invent numbers like “A Gazillion Bazillionâ€. But there is a lot of more to infinity than merely counting on forever.
The first person who wrestled with the murky idea of infinity was Georg Cantor. He was the inventor of “set theory†and was the first person to define infinite sets. His theories of infinity were never fully accepted until the 20th century. Henri Poincare, the great French mathematician called Cantor's work, “ a grave disease†while Leopold Kronecker called him, a “corrupter of youthâ€. The fierce criticism of his work eventually led him to the sanatorium where he died in poverty. No starker contrast between the beauty of the ideas and the squalor of one's life can be found. His most surprising result was that there are different kinds of infinity and that some infinities, despite looking different, are actually the same.
The simplest case where this phenomenon occurs is this: the infinity corresponding to the set of rationals is the same as the infinity corresponding to the set of integers. On the other hand, the infinity corresponding the reals is bigger than that of the rationals or the integers. Here is a video that lays out the arguments for both claims.
Let’s consider adding fractions. We all know that if we add two fractions we get another fraction. If we add three fractions, what happens? Well, we get another fraction. Now, consider adding a finite number of fractions, will the result be a fraction? Again the answer is yes. Here comes the rub: let's say we add fractions an infinite number of times, do we get a fraction ? The answer is “not alwaysâ€. Consider the following addition of fractions: 
. This is a well known formula for the number 
which is the base for the natural logarithm. It is a theorem that this number is not equal to any fraction.
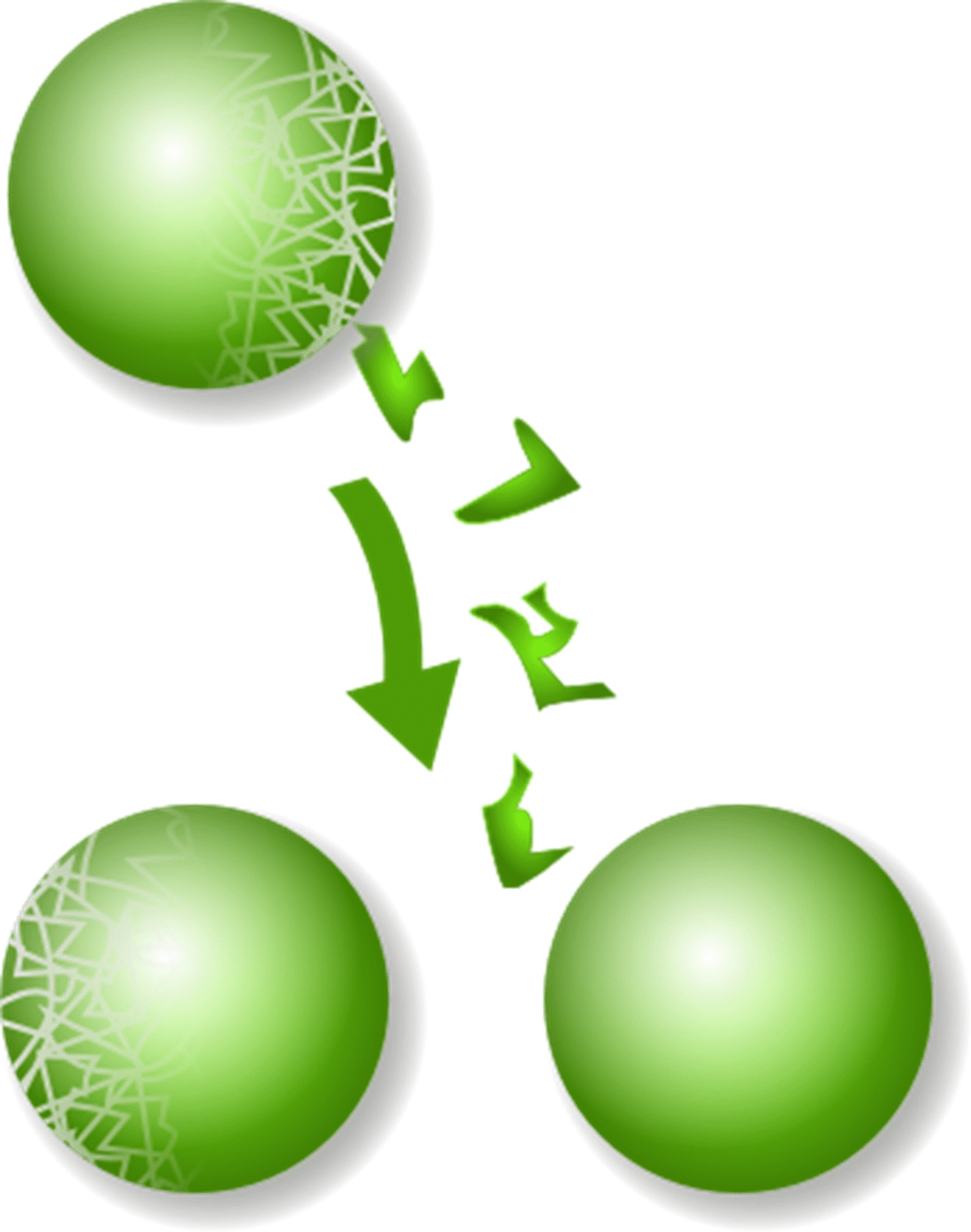
The last mind altering encounter with infinity can be explained with the following thought experiment : suppose we have a solid ball in 3 dimensional space and we imagine disintegrating it into all its points. We then move and rotate its points such that we create two solid balls. We now ask the question, “What is the volume of the combined two balls?” The answer of course seems trivial, the volume of the two balls is the volume of the original solid ball. But what Stefan Banach and Alfred Tarski found is that in 3 dimensions, each of the two balls have the same volume as the original ball. This is the famous Banach Tarski paradox. The reasons for this paradox are complicated, but suffice it to say the culprit is the appearance of an uncountable number of sets in 3 dimensions for which we can’t consistently assign a meaningful notion of volume. The technical term for these sets is “non-measurable sets.â€
In conclusion, what lesson can we learn? Infinity is an incredibly slippery notion with highly unintuitive properties. So the next time you find yourself in a spacey mood contemplating how everything is infinite, take a step back. There is a good chance your ideas can’t be made coherent or even defined correctly. Infinity is more than just an unending process.
About the author
 |
Amara Katabarwa is a PhD candidate in the Physics and Astronomy Department at the University of Georgia studying His research focus is understanding Decoherence in Quantum Circuits and near term application of first generation Quantum Computers. In his free time he likes to read or guiltlessly laze about. He can be contacted at akataba@uga.edu. |
